Paper Review: QA-LoRA: Quantization-Aware Low-Rank Adaptation of Large Language Models

Paper Review: LAVIE: QA-LoRA: Quantization-Aware Low-Rank Adaptation of Large Language Models

Paper link

Code link

Large language models have seen rapid growth in recent years, but their computational demands limit their use on edge devices. This paper introduces a method called quantization-aware low-rank adaptation (QA-LoRA). It balances the challenges of quantization and adaptation using group-wise operators. With just a few lines of code, QA-LoRA allows LLMs to be fine-tuned with quantized weights (like INT4) to save time and memory. After fine-tuning, the LLM and extra weights merge into a quantized model without losing accuracy. The method is tested on the LLaMA and LLaMA2 models across various datasets and applications, proving its effectiveness.

The proposed approach

Baseline: low-rank adaptation and low-bit quantization

In LoRA, the weight matrix is W and the feature vector is x. LoRA introduces two matrices, A and B, to supplement W. During fine-tuning, the computation is y = W^T * x + s * (A * B)^T * x, where s is a tuning coefficient, W remains constant, and A and B are adjustable. After fine-tuning, the formula becomes y = (W + s * A * B)^T * x, with W replaced by W' = W + s * A * B for faster inference.

To reduce computational costs, low-bit quantization is employed, specifically the min-max quantization method. This approach quantizes the weight matrix W into W~ using scaling and zero factors α and β, and integer rounding. This quantization reduces storage needs and speeds up computation, but it introduces approximation errors. To minimize these errors, individual quantization for each column of W is recommended. This method updates the computation and storage requirements while preserving approximation accuracy.

Objective: efficient adaptation and deployment

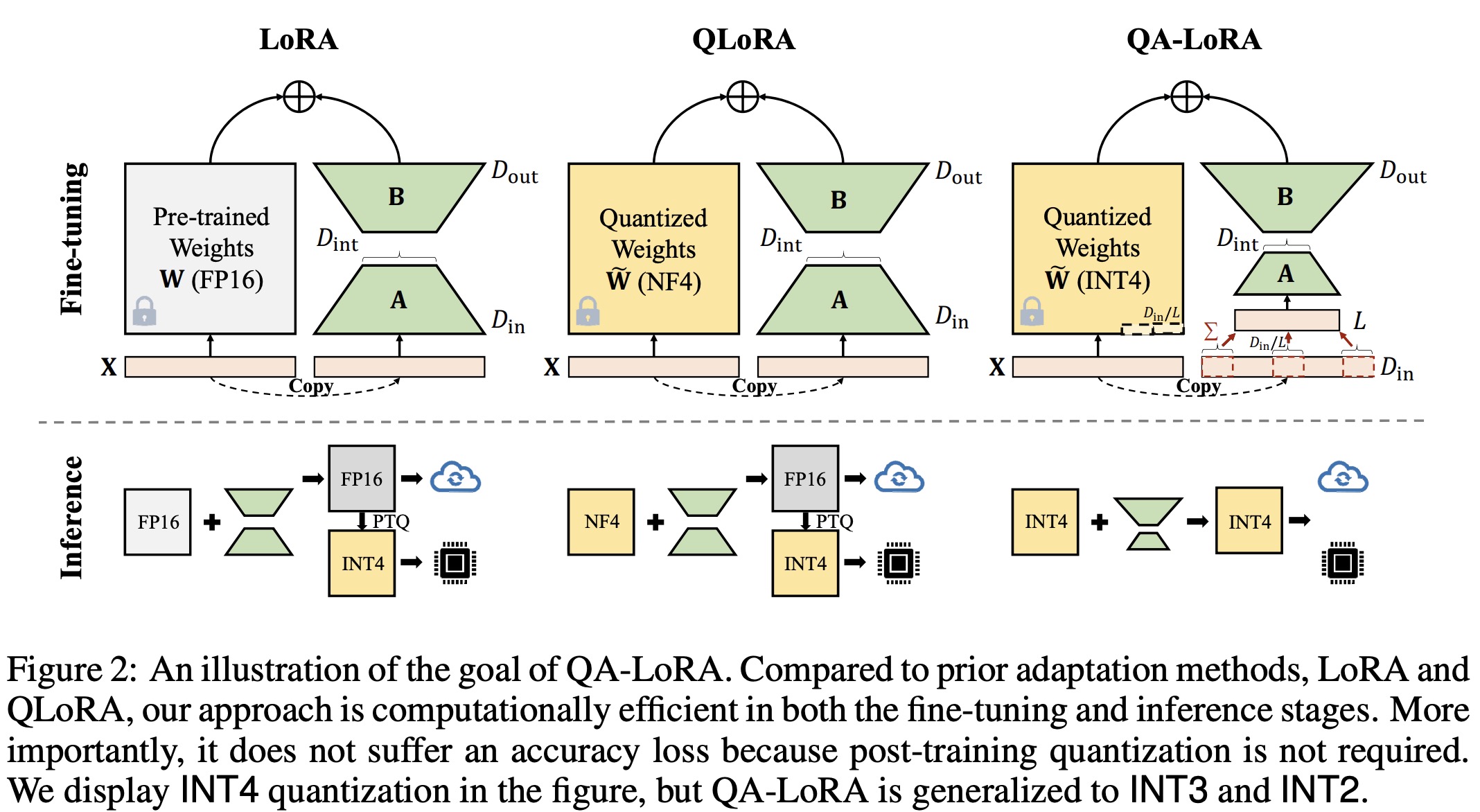
The main objective is twofold:

• During fine-tuning, the pretrained weights W are converted to a low-bit format to allow LLMs to be fine-tuned using minimal GPUs.
• Post fine-tuning, the adjusted and combined weights W' remain in a quantized format for efficient LLM deployment.
• QLoRA, a recent LoRA variant, achieved the first goal by quantizing W from FP16 to NF4 during fine-tuning. This joint optimization of quantization and adaptation is feasible as the accuracy difference between W and W~ is offset by the low-rank weights s * AB. However, after fine-tuning, the side weights s * AB are reintegrated to W~, reverting the final weights W' to FP16. Post-training quantization on W' can lead to notable accuracy loss, especially with a low bit width. Moreover, there’s no current optimization for NF4, hindering acceleration during fine-tuning and inference. Thus, QLoRA’s primary advantage is reducing memory usage during fine-tuning.

Solution: group-wise quantization with low-rank adaptation

The primary objective is to merge the quantized W~ and s * AB without resorting to high-precision numbers like FP16. In the original setting, this is unattainable due to the column-wise quantization of W and the unconstrained nature of matrices A and B. The first idea of the authors requires all row vectors of A to be identical. However, this approach results in a significant accuracy drop since it limits the rank of AB to 1, affecting the fine-tuning ability.

To address this, the constraints for both quantization and adaptation are relaxed. W is partitioned into L groups, and individual scaling and zero factors are used for quantization within each group. This also requires row vectors of A within the same group to be identical. The approach requires minimal code changes. Compared to LoRA and QLoRA, QA-LoRA offers time and memory benefits. It requires extra storage for scaling and zero factors but reduces the parameters of A.

Experiments

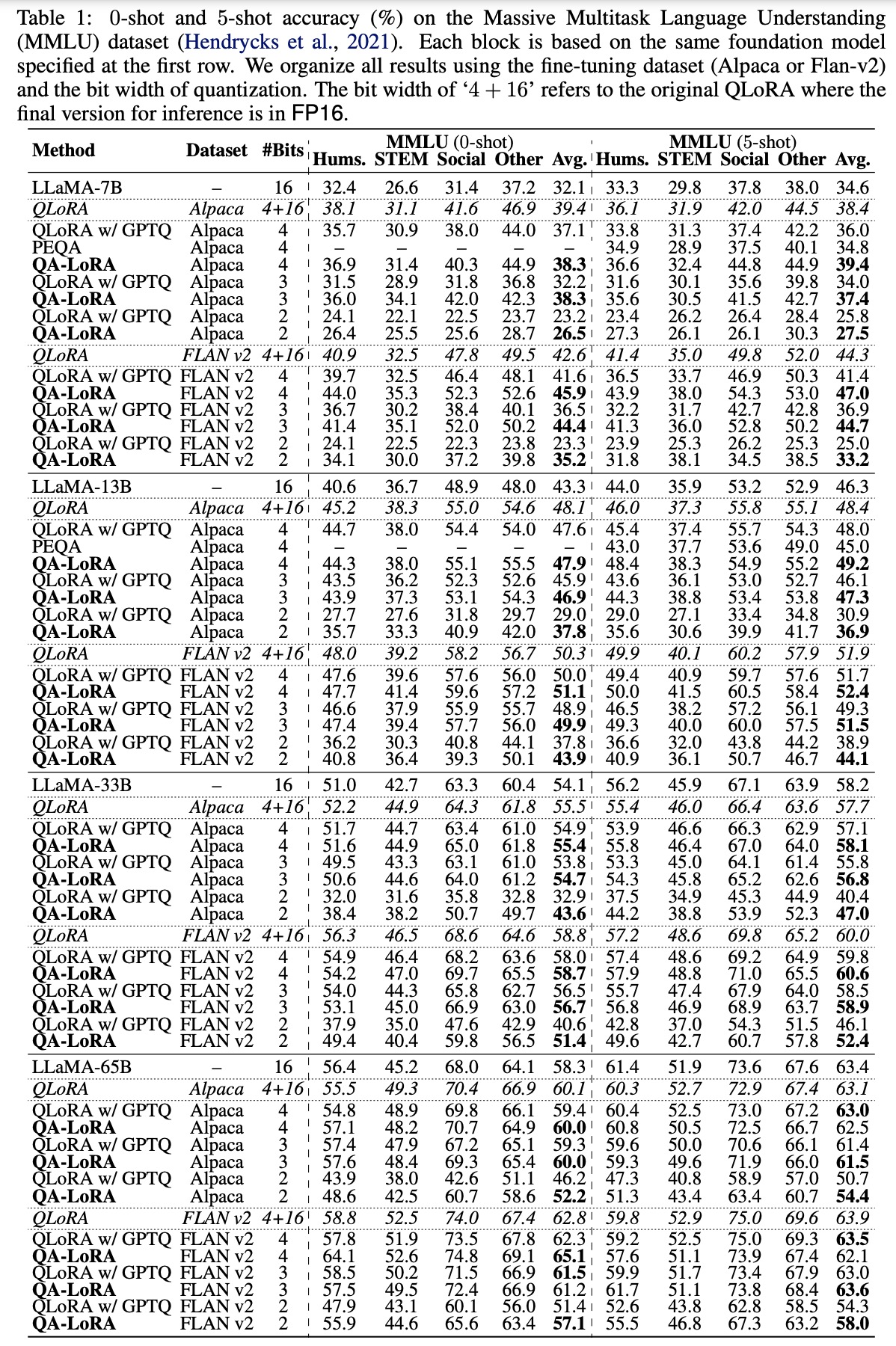
• QA-LoRA consistently outperforms its competitors, QLoRA and PEQA, in both 0-shot and 5-shot accuracy. The superiority of QA-LoRA is especially evident with smaller model sizes or when using lower bit widths, highlighting its efficiency. In some instances, the INT4 version of QA-LoRA even surpasses the original QLoRA in performance while being faster in inference. The primary advantage of QA-LoRA stems from its quantization-aware adaptation, which compensates for post-training quantization, leading to more stable results.
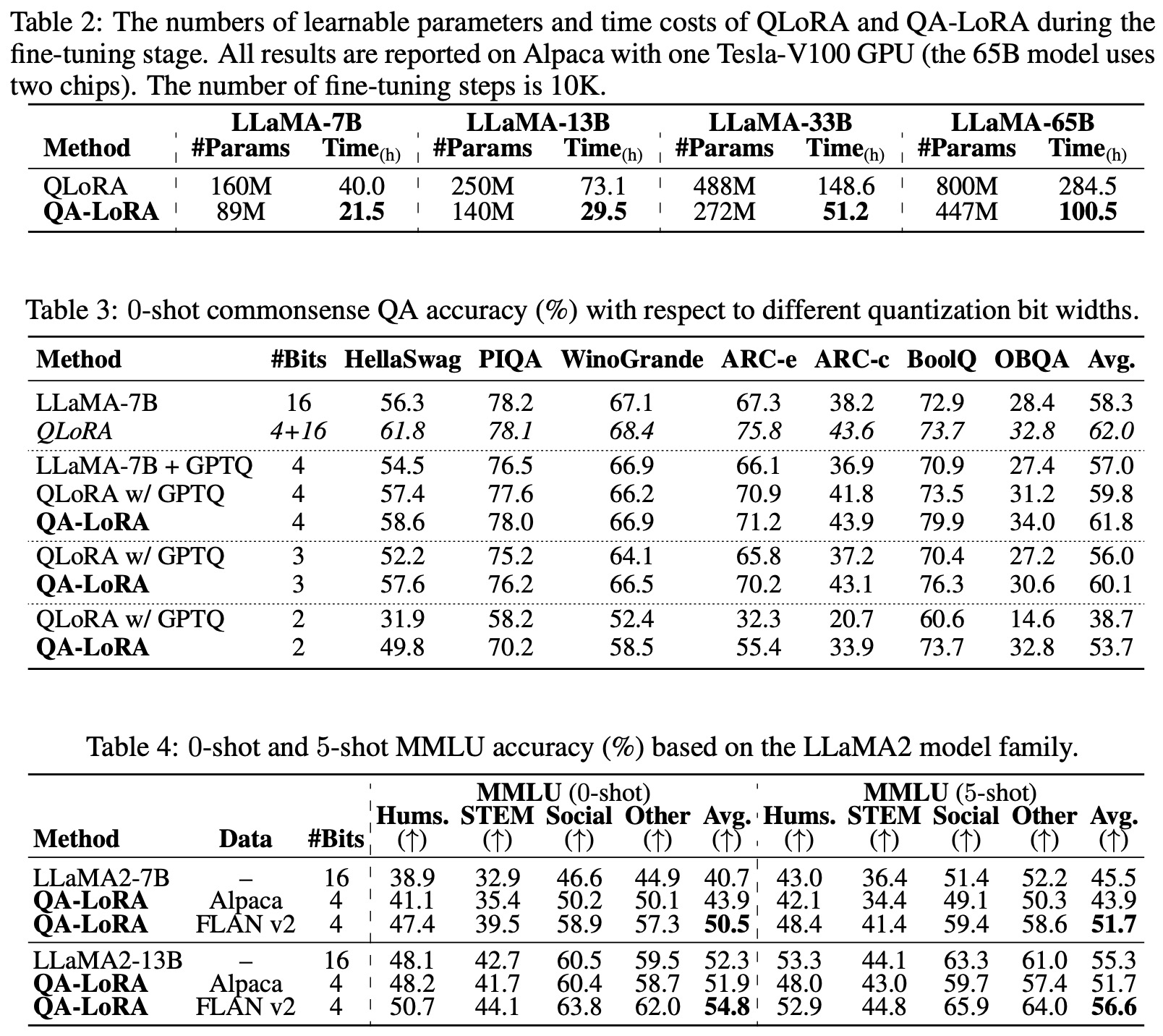
• During fine-tuning, QA-LoRA’s significant time advantage is attributed to its use of INT4 quantization, which is optimized by CUDA and faster than QLoRA’s NF4 quantization. In the inference stage, QA-LoRA is over 50% faster than QLoRA since it remains in INT4, while QLoRA reverts to FP16.
• For commonsense QA based on LLaMA-7B, 4-bit QA-LoRA matches mixed-precision QLoRA and surpasses post-quantized QLoRA by an average of 2.0%. The advantage is even more pronounced in low-bit scenarios, with 2-bit QA-LoRA achieving a 15.0% accuracy boost over its counterpart.
• when applied to LLaMA2 models, QA-LoRA demonstrates its effectiveness and generalizability. The INT4 models fine-tuned with FLAN v2 consistently outperform the original FP16 models, while those with Alpaca show slightly reduced accuracy. This confirms QA-LoRA’s applicability across different pre-trained model families.

Ablations:

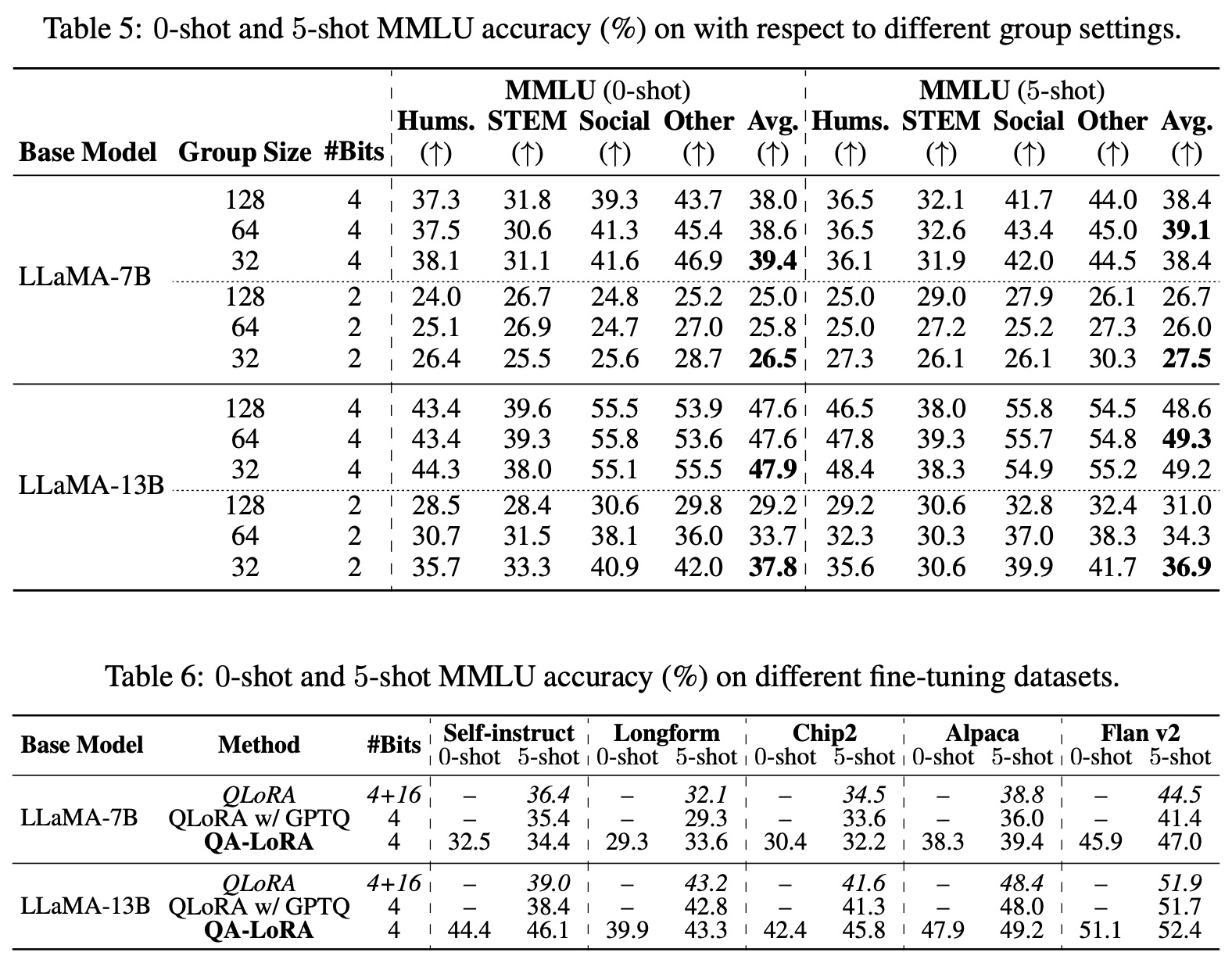
• Quantization Group Size: A larger L (meaning a smaller group size) often results in better accuracy. This advantage is more pronounced with smaller quantization bit widths, suggesting that greater quantization loss benefits from increased degrees of freedom.
• Fine-tuning Datasets: QA-LoRA’s performance was evaluated on additional datasets like Selfinstruct, Longform, and Chip2. These datasets are smaller compared to Alpaca and FLAN v2, leading to slightly reduced accuracy on MMLU. However, using LLaMA-13B as the base model, QA-LoRA consistently outperformed QLoRA with mixed precision and was faster during inference.
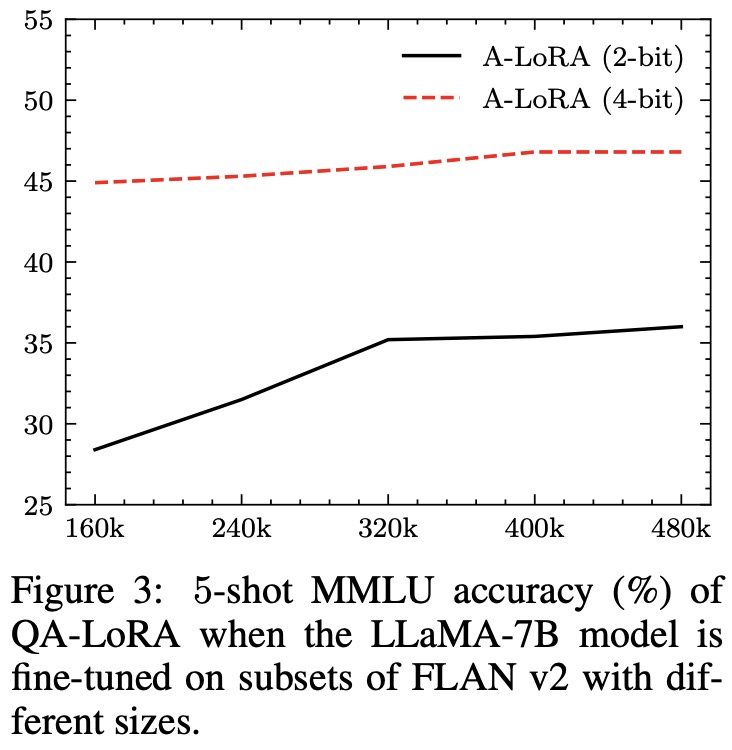
• Size of Fine-tuning Datasets: Low-bit quantization requires more data. However, a dataset size of 320K is adequate for both the INT2 and INT4 versions of QA-LoRA.

Qualitative studies