Paper Review: Explaining grokking through circuit efficiency

Paper Review: Explaining grokking through circuit efficiency

Paper link

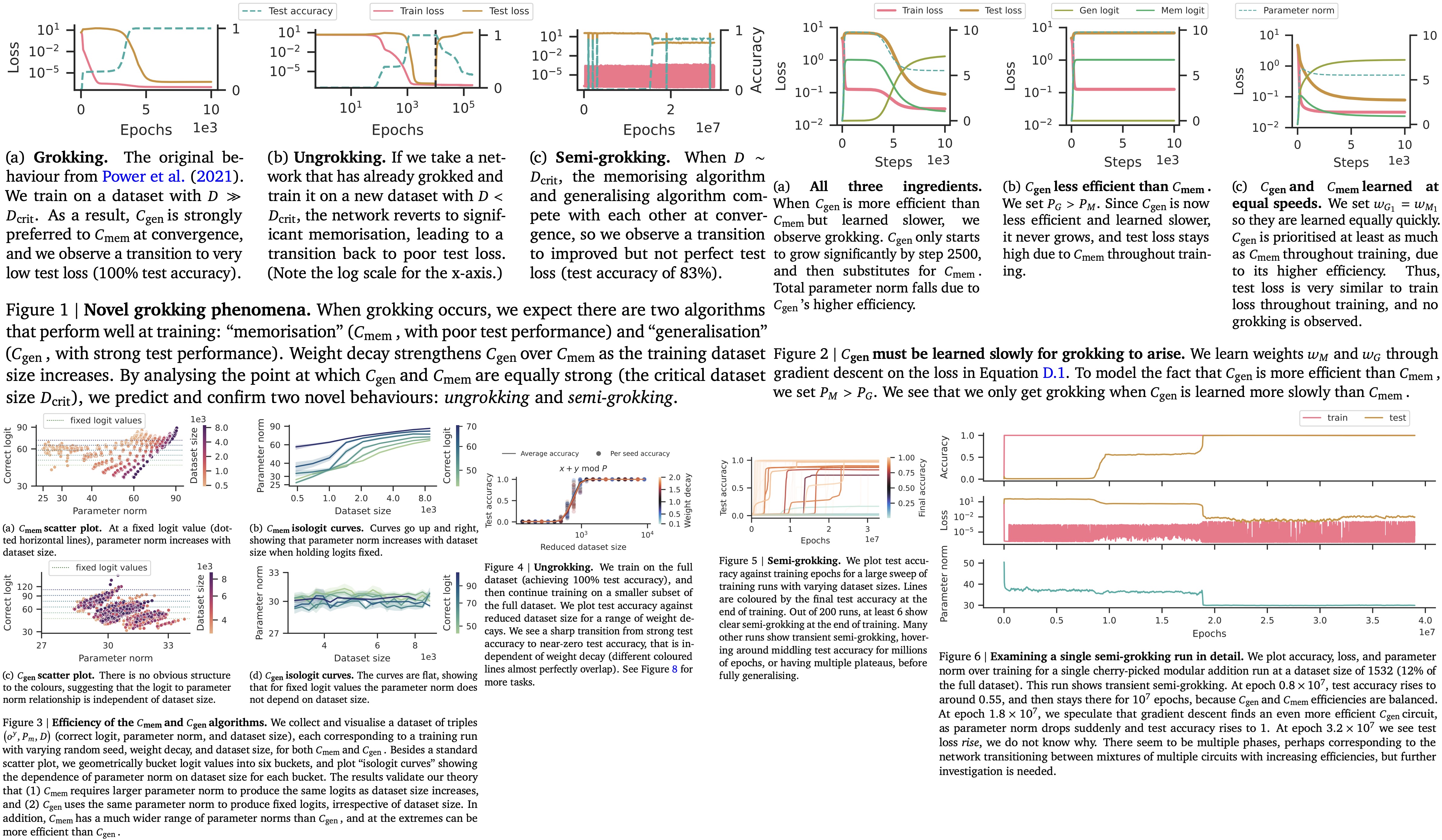
The concept of “grokking” refers to a phenomenon in neural networks where a network that initially memorizes the training data but performs poorly on new, unseen data eventually learns to generalize well after further training. The authors propose that this happens because there are two kinds of solutions a neural network can learn: a memorizing solution and a generalizing solution. The generalizing solution is slower to learn but ultimately more efficient and produces better results on new data.

The hypothesis is that the efficiency of memorizing circuits decreases as the dataset grows larger while generalizing circuits maintain their efficiency. This implies there is a critical dataset size where both memorization and generalization would be equally efficient.

The authors test and confirm four new predictions about this grokking behavior. It also observes two surprising behaviours: Ungrokking, where a network initially generalizes well but then regresses back to poor generalization. Semi-grokking, where a network eventually learns to generalize but only to a limited extent, rather than achieving perfect generalization.

Three ingredients for grokking

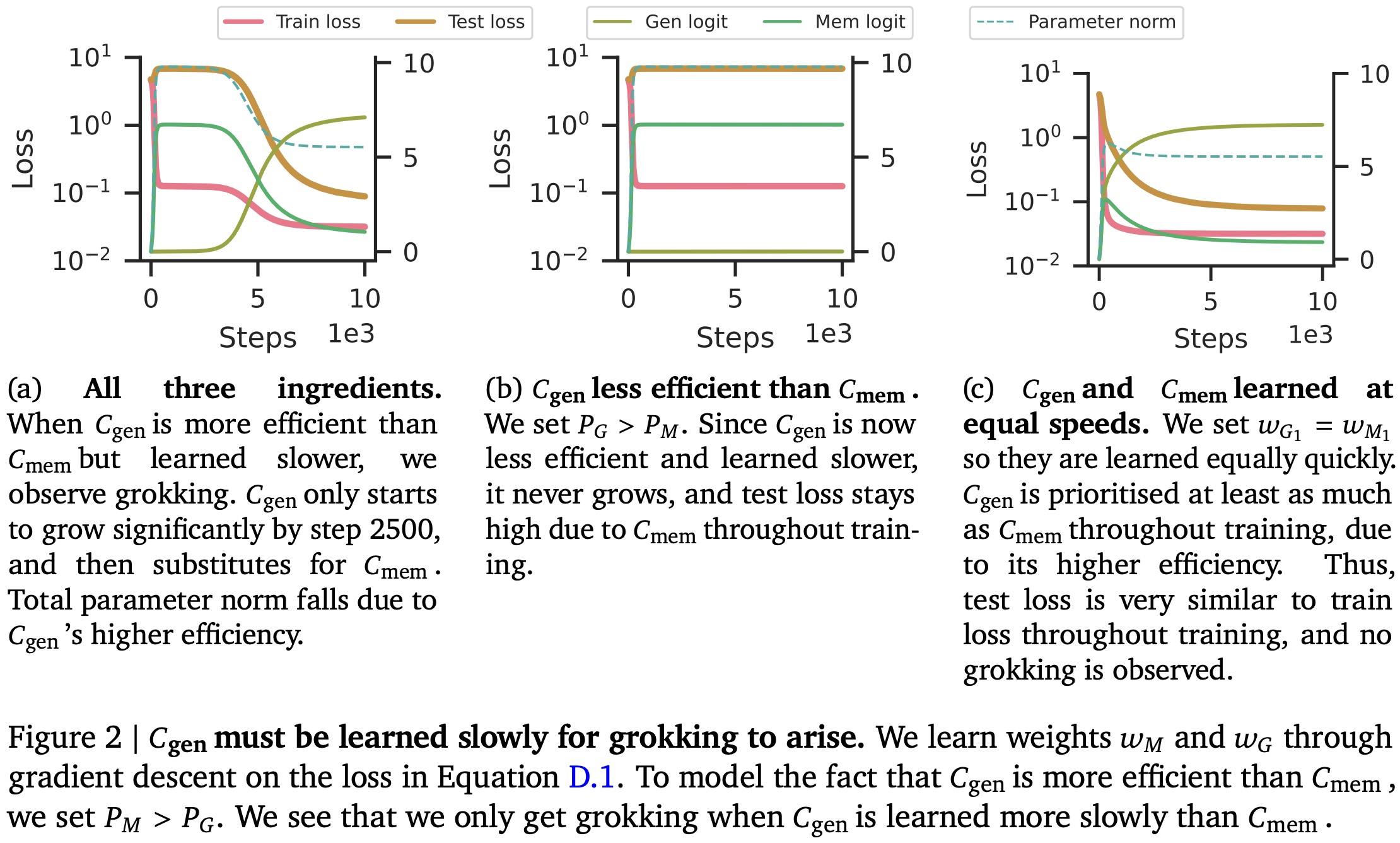
In the concept of grokking within neural networks, two types of circuits (internal mechanisms that neural nets use to calculate the outputs) exist one for memorizing data and another for generalizing. Both circuits are influenced by two opposing forces. Cross-entropy loss drives the classifier’s logits to increase in size to boost the model’s confidence, while weight decay works to reduce the model’s parameters. These forces must be balanced to achieve any local minimum in the loss function.

Grokking occurs when three key elements are present:

• Generalizing and Memorizing Circuits: Both types of circuits can offer good training performance, but only the generalizing circuit performs well on unseen test data.
• Efficiency: The generalizing circuit is more efficient than the memorizing circuit, meaning it achieves the same level of cross-entropy loss on the training set but with fewer parameters.
• Learning Speed: The generalizing circuit is slower to learn than the memorizing circuit. As a result, early in training, the faster-learning memorizing circuit dominates but offers poor test performance.

The process of grokking unfolds in two phases: Initially, the memorizing circuit is quickly learned, which leads to strong training performance but poor test performance. As training progresses, the more efficient but slower-learning generalizing circuit starts to take over. This “reallocates” the parameter norm from the memorizing to the generalizing circuit, leading to improved generalization on test data.

Experimental evidence confirms that when all these three ingredients are in place, standard grokking behavior is observed. If any of these elements are missing or altered, the model fails to exhibit the grokking phenomenon.

Why generalising circuits are more efficient

Relationship of efficiency with dataset size

When training classifiers on datasets, adding more data doesn’t necessarily make the classifier more efficient. Efficiency, in this context, tends to be stable or even decrease as dataset size increases. If a classifier can generalize well, its efficiency will likely remain consistent, even when new data points are introduced. However, if the classifier fails to generalize, its efficiency will probably drop as it struggles to adapt to new information.

A generalizing circuit can maintain its efficiency because it doesn’t need to change its parameters significantly to adapt to new data. On the other hand, a memorizing circuit tends to lose efficiency as the dataset grows since it needs to adjust its parameters for each new data point.

The efficiency of these circuits as a function of dataset size introduces the concept of a “critical dataset size”. Below this threshold, memorizing circuits tend to be more efficient because they can easily adapt to a small amount of data. Above this threshold, generalizing circuits gain the upper hand in efficiency, which can result in “grokking,” or a sudden leap in understanding or performance by the model.

Interestingly, the strength of weight decay—regularization to prevent overfitting—doesn’t affect this critical threshold. While it may influence other aspects of the model, weight decay doesn’t change the point at which generalizing circuits become more efficient than memorizing ones. Therefore, understanding the interplay between dataset size, classifier efficiency, and weight decay can provide insights into when grokking is likely to occur.

Implications of crossover: ungrokking and semi-grokking

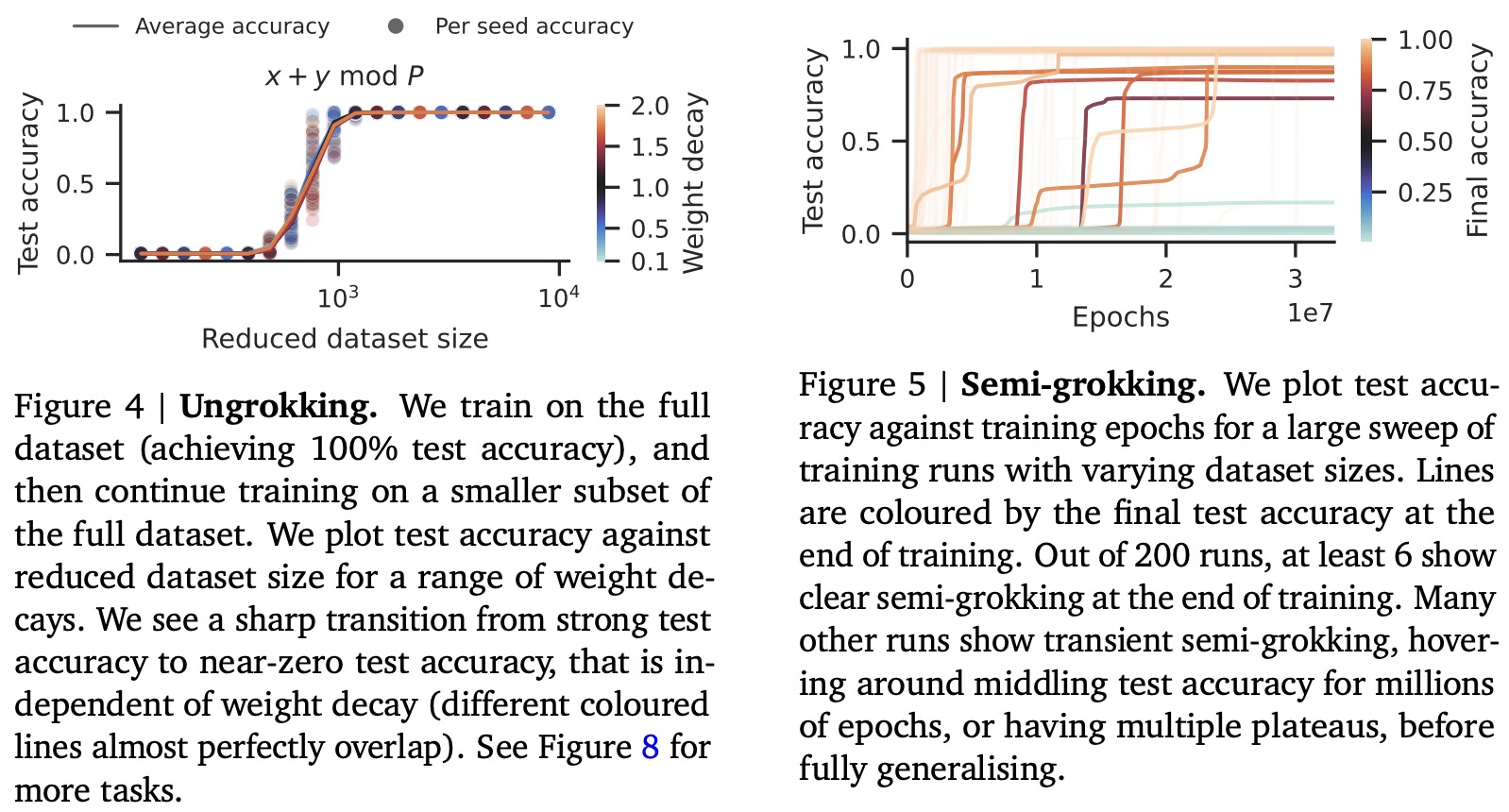
Ungrokking occurs when a network trained on a larger dataset (exceeding critical size) is trained further on a smaller dataset (smaller than critical size). In this new context, memorizing circuits become more efficient than generalizing circuits, leading to a decrease in test performance. This contrasts with grokking, where test performance improves. Ungrokking can be seen as a special case of catastrophic forgetting, although with certain differences:

• It is expected only at datasets smaller than critical size;
• It can happen not only when adding new samples but also when removing existing ones;
• The magnitude of forgetting doesn’t depend on weight decay;

Semi-grokking happens when a network is trained on a dataset size close to the critical size, where both circuits are similarly efficient. There are two potential outcomes: either one of the circuits will dominate, leading to either the presence or absence of grokking, or a mix of both circuits will arise, leading to middling test performance. In this second scenario, the network will initially show good training but bad test performance, followed by an improvement in test performance, which is termed semi-grokking.

Experiments

The authors train 1-layer Transformer model with AdamW on the modular addition tasks.

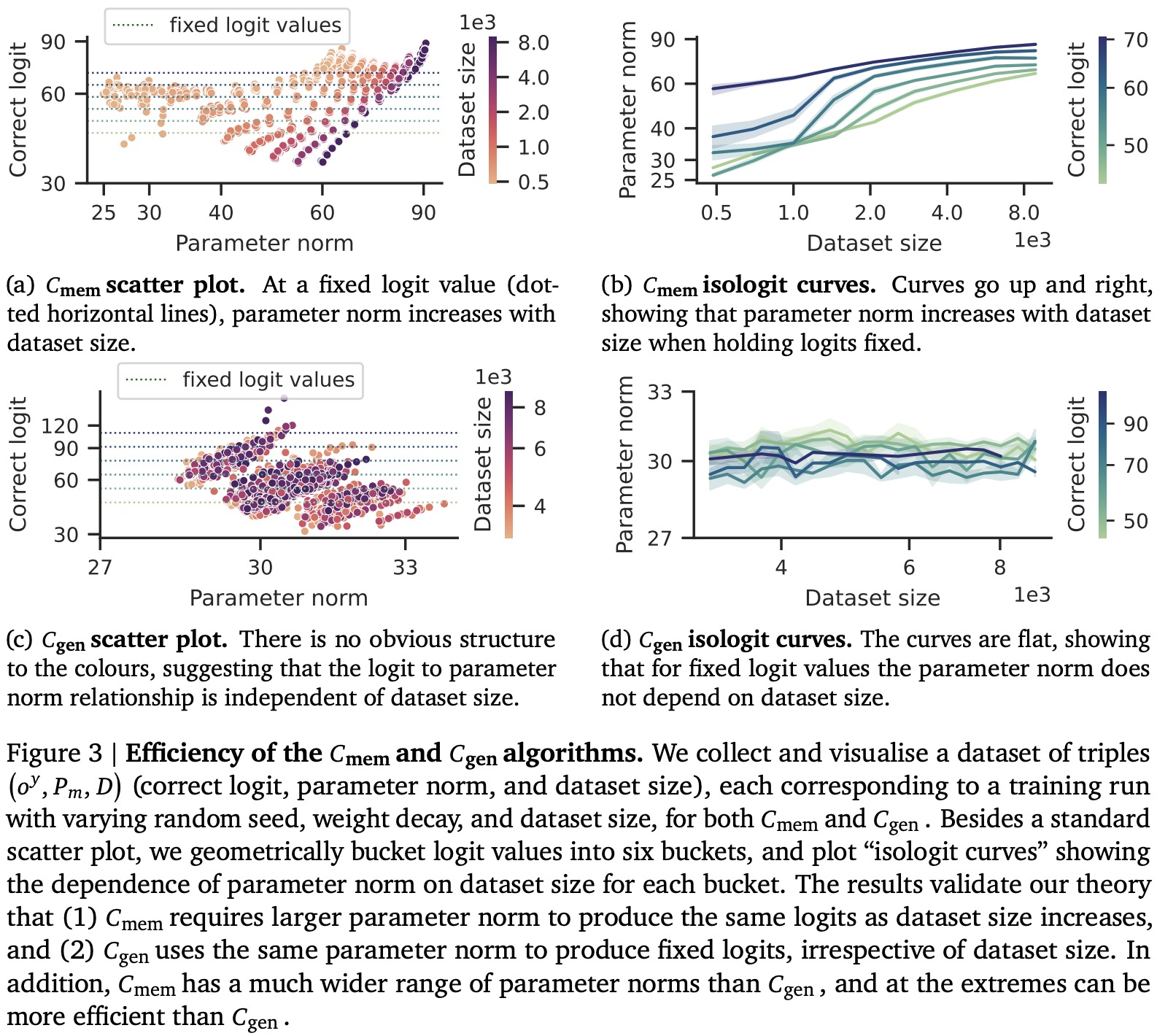
• Increased dataset size leads to decreased memorization efficiency, requiring higher parameter norms for the same logit values. On the other hand, for generalization, the parameter norm remains the same regardless of dataset size. The results also indicate that varying efficiencies can occur due to different random seeds during initialization;
• Experiments confirm the existence of ungrokking and semi-grokking;

Discussion

The authors offer a resolution to the question of why deep neural networks can generalize well even when they can easily memorize random labels. They suggest that circuits designed for generalization are more efficient than those for memorization when the dataset is large enough and weight decay is present. However, they acknowledge limitations, such as the reliance on weight decay for its explanation and the consideration of only one kind of constraint, the parameter norm. Grokking has been observed even without weight decay, suggesting that other regularizing effects may be at play.

I want to add a personal opinion: while I think that this is a fascinating paper, I feel that there should have been more experiments in realistic settings. And the authors themselves acknowledge that they rely on the weight decay too much.