Paper Review: mHC: Manifold-Constrained Hyper-Connections
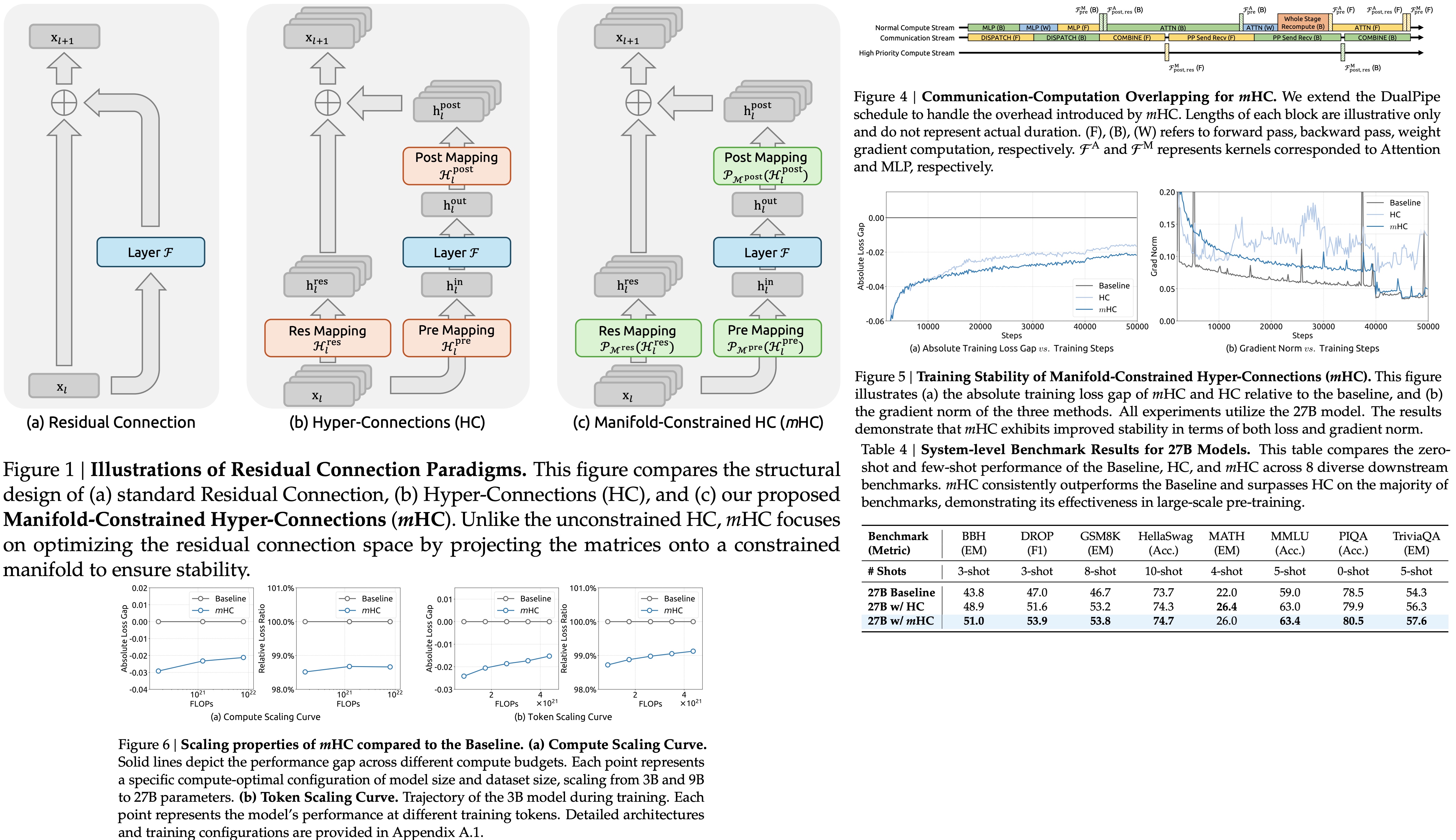
Hyper-Connections (HC) architectures expand residual streams and diversify connectivity patterns beyond traditional residual blocks but break the identity mapping property, causing training instability, poor scalability, and inefficient memory access. The authors propose Manifold-Constrained Hyper-Connections (mHC), a general framework that projects HC residual connections onto a defined manifold to restore identity mapping while retaining the expressivity of HC. The design incorporates infrastructure-level optimizations to keep memory and computational costs low.
Empirical evaluation shows that mHC trains robustly at scale, improves performance across tasks, and scales better than prior HC variants without sacrificing efficiency.
Introduction
Residual connections are widely used in modern deep networks because their identity mapping property lets signals pass unchanged across layers, stabilizing training at scale. Hyper-Connections extend this idea by widening the residual stream into multiple parallel channels and learning how to mix them, increasing expressivity and topological complexity without raising per-layer FLOPs. However, this unconstrained mixing breaks the identity mapping property: across many layers, the residual transformations no longer preserve the global mean of the signal, leading to amplification or attenuation and training instability. In addition, the widened residual stream introduces significant memory-access overhead. As a result, despite their performance potential, Hyper-Connections are unstable and hard to scale in large training regimes.
The approach
Manifold-Constrained Hyper-Connections
mHC restores stable signal propagation by constraining the residual mixing matrix onto a specific manifold rather than leaving it unconstrained as in Hyper-Connections. Instead of forcing the residual mapping to be the identity, which would block interaction between streams, it is restricted to be a doubly stochastic matrix, with non-negative entries and rows and columns summing to one. This preserves the identity mapping behavior in a generalized form while still allowing information exchange across streams.
Doubly stochastic matrices are non-expansive, which limits gradient explosion, and they are closed under multiplication, so stability is preserved across many layers. Geometrically, they form the Birkhoff polytope, meaning each residual mapping acts as a convex combination of permutations and gradually increases mixing across streams, functioning as robust feature fusion. Additional non-negativity constraints on the input and output projection matrices prevent signal cancellation and further stabilize training.
Parameterization and Manifold Projection
At each layer, the hidden state is flattened into a single vector and passed through RMSNorm to generate dynamic mixing weights, following the original Hyper-Connections setup. Linear projections produce unconstrained versions of the input mapping, output mapping, and residual mixing matrix. The input and output mappings are then passed through a sigmoid to enforce non-negativity, while the residual mixing matrix is projected onto the manifold of doubly stochastic matrices using the Sinkhorn–Knopp algorithm. This projection exponentiates the matrix to make all entries positive and then iteratively normalizes rows and columns to sum to one, converging to a doubly stochastic matrix after a fixed number of steps. In practice, about 20 normalization iterations are used to obtain the final constrained residual mapping.
Efficient Infrastructure Design
To reduce mHC overhead, the authors reorder the normalization step to follow matrix multiplication. This preserves mathematical equivalence while lowering latency on high-dimensional inputs. They use mixed-precision to balance numerical accuracy and speed, and fuse operations with shared memory access into unified compute kernels to alleviate memory bandwidth bottlenecks. Three specialized kernels compute the input mapping, output mapping, and residual mixing matrix, with biases, projections, and RMSNorm weights absorbed into consolidated parameters. Additional fusion combines multiple scans, lightweight coefficient operations, and the Sinkhorn–Knopp iteration into single kernels. The custom backward pass recomputes intermediate results on-chip. Two further kernels apply the mappings, with residual merging fused to drastically cut memory reads and writes. Most kernels are implemented with TileLang, enabling efficient handling of complex computations while maximizing memory bandwidth utilization with minimal engineering overhead.
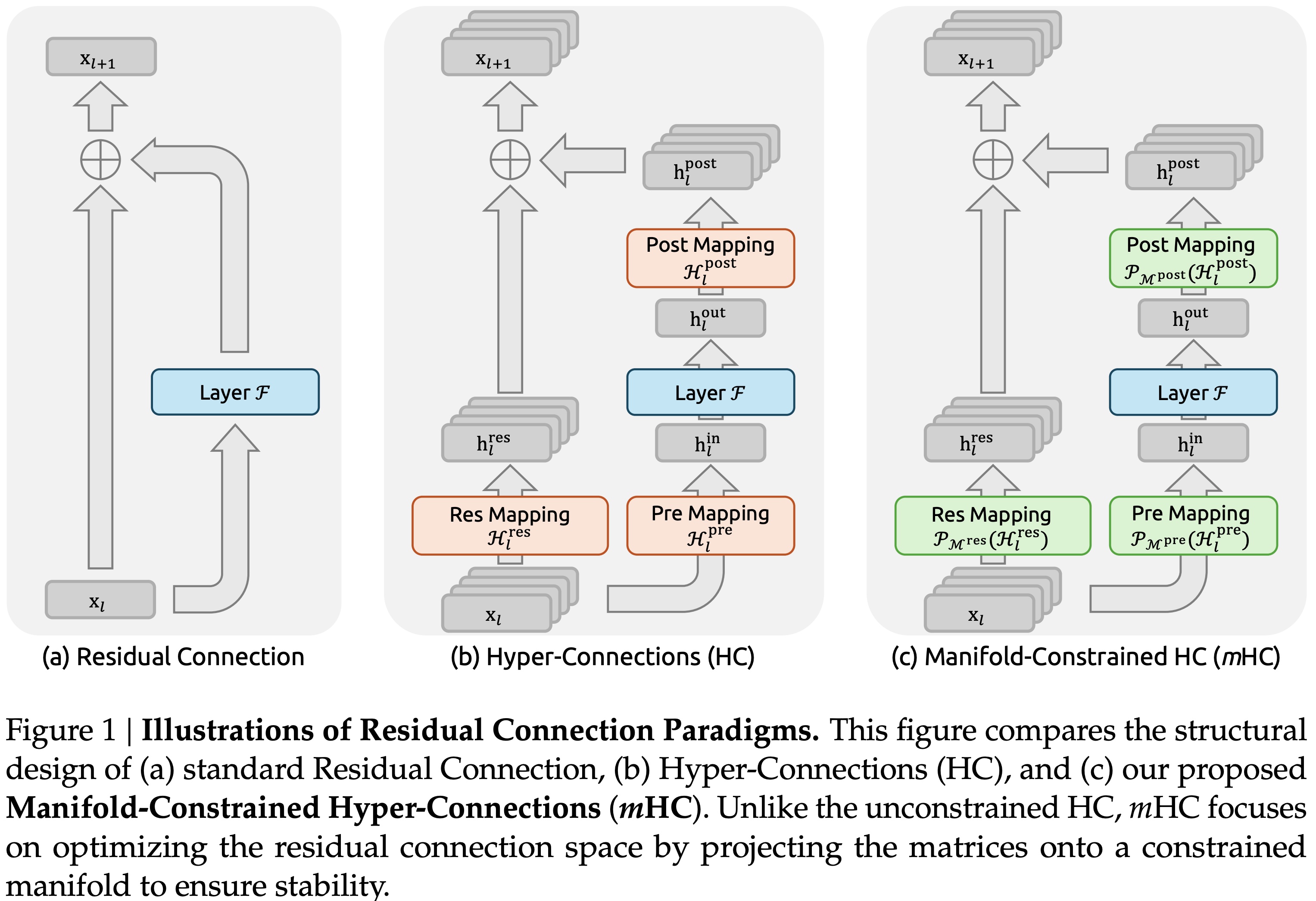
The n-stream residual design greatly increases memory usage, so mHC drops all intermediate activations after the forward pass and recomputes them during backpropagation by rerunning the mHC kernels without the expensive layer function. For each block of consecutive layers, training stores only the input to the first layer, which reduces resident memory.
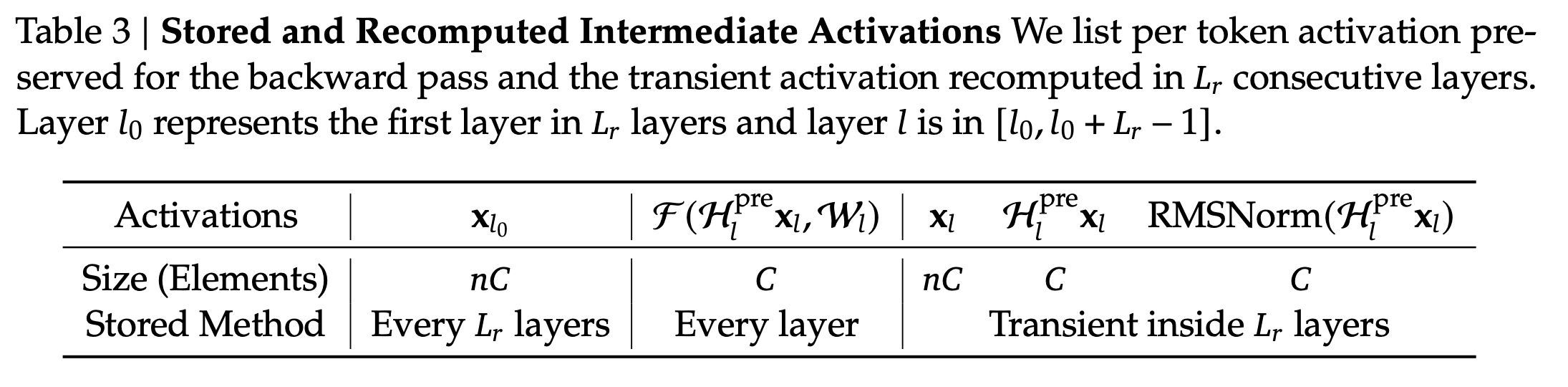
Pipeline parallelism with the DualPipe schedule overlaps communication and computation, but the n-stream residual design in mHC adds significant cross-stage communication latency and extra recomputation cost at stage boundaries. To reduce these bottlenecks, the authors extend the schedule to improve overlap between communication and computation when entering new pipeline stages. The kernels in MLP layers run on a dedicated high-priority compute stream to avoid blocking communication, while long persistent kernels in attention layers are avoided to prevent stalls and allow preemption.
Experiments
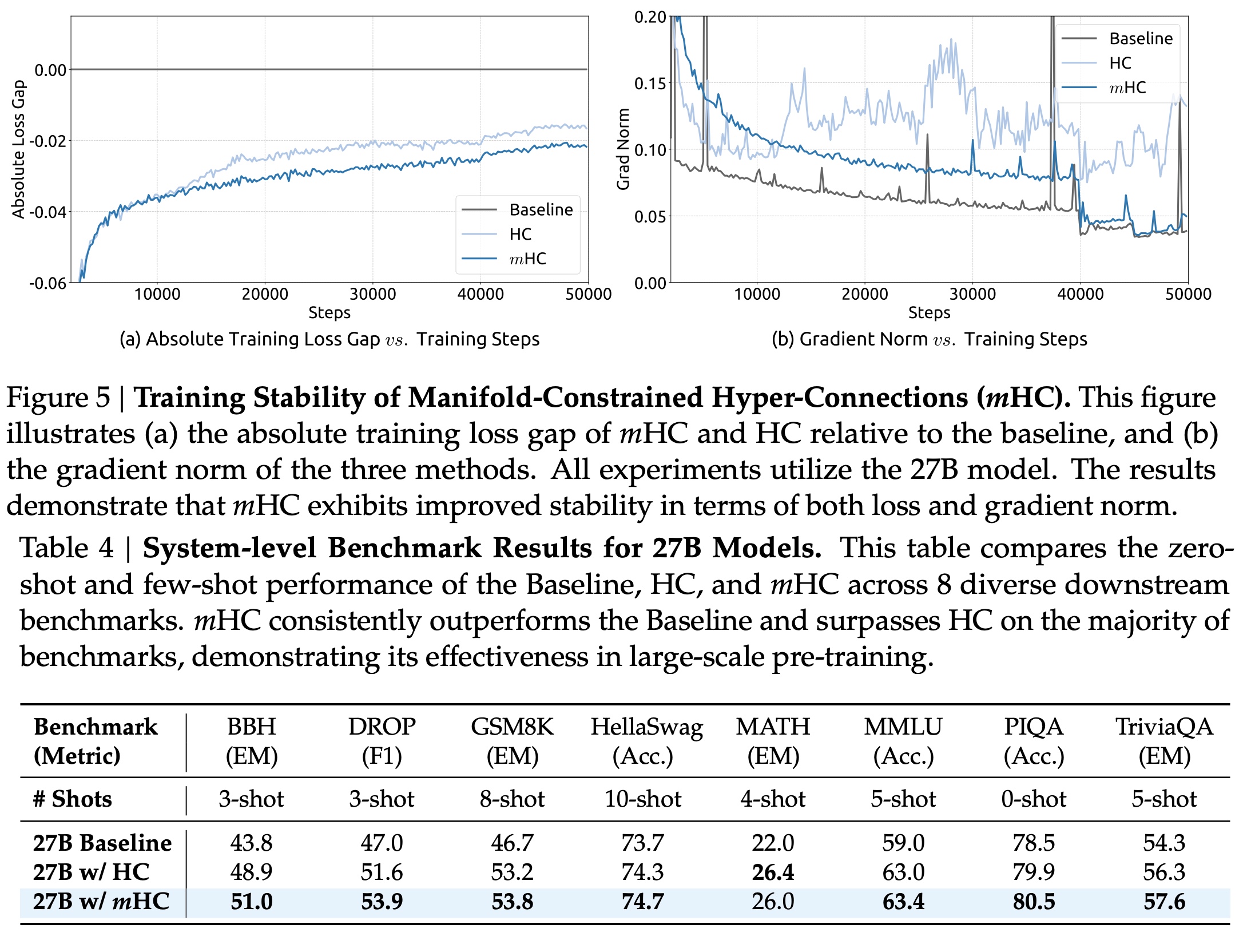
mHC effectively mitigates the training instability observed in HC and yields comprehensive improvements on the downstream benchmarks.
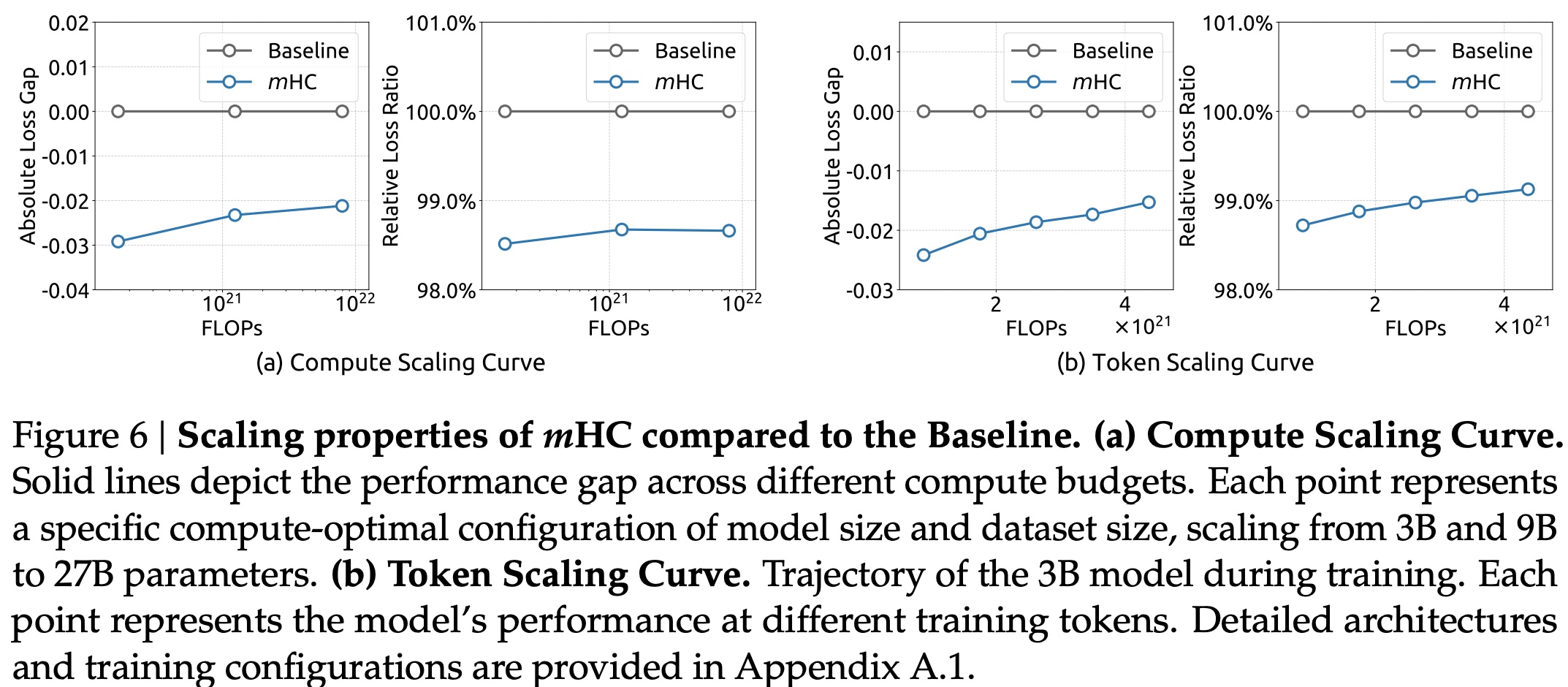
The performance advantage is robustly maintained even at higher computational budgets, which proves the effectiveness of mHC in large-scale scenarios.
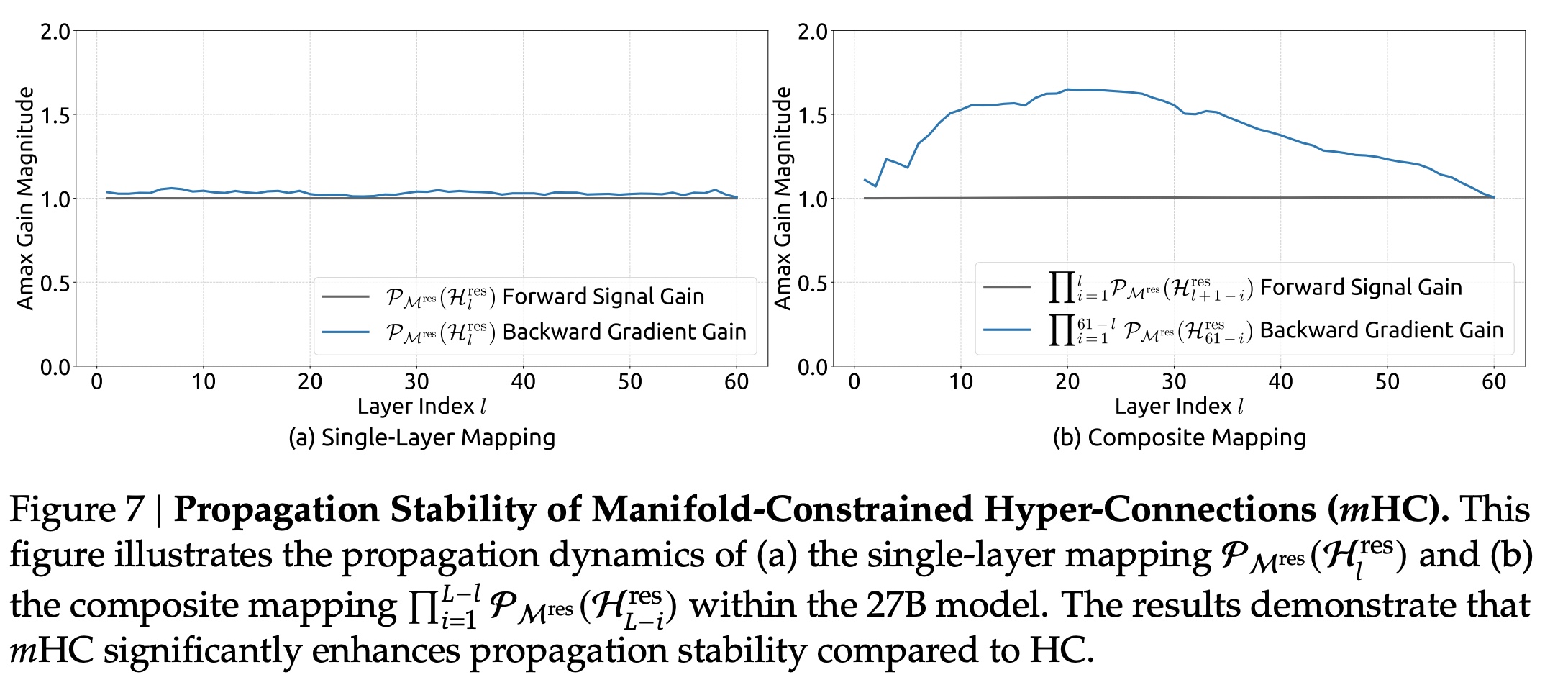
mHC maintains much more stable signal and gradient propagation than Hyper-Connections.
You can read my review on DeepSeek-R1 here.
paperreview deeplearning architecture llm nlp